Drawing on Complexity to do Hands-on Evaluation (Part 3) – Turning the Wrench

Common Introduction to all Three Posts
What is the Contribution of Complexity to Evaluation?
Drawing from Research and Theory in Complexity Studies

Common Introduction to all Three Posts

This is the third of three blog posts I have been writing to help me understand how “complexity” can be used in evaluation. If it helps other people, great. If not, at least it helped me.

Part 1:  Complexity in Evaluation and in Studies on Complexity
In this section I talked about using complexity ideas as practical guides and inspiration for conducting an evaluation, and how those ideas hold up when looked at in terms of what is known from the study of complexity. It is by no means necessary that there be a perfect fit. It’s not even a good idea to try to make it a perfect fit. But the extent of the fit can’t be ignored, either.

Part 2: Complexity in Program Design
The problems that programs try to solve may be complex. The programs themselves may behave in complex ways when they are deployed. But the people who design programs act as if neither their programs, nor the desired outcomes, involve complex behavior. (I know this is an exaggeration, but not all that much. Details to follow.) It’s not that people don’t know better. They do. But there are very powerful and legitimate reasons to assume away complex behavior. So, if such powerful reasons exist, why would an evaluator want to deal with complexity? What’s the value added in the information the evaluator would produce? How might an evaluation recognize complexity and

Part 3: Turning the Wrench: Applying Complexity in Evaluation
This is where the “turning the wrench” phrase comes from in the title of this blog post1. Considering what I said in the first two blog posts, how can I make good use of complexity in evaluation? In this regard my approach to complexity is no different than my approach to ANOVA or to doing a content analysis of interview data. I want to put my hands on a tool and make something happen. ANOVA, content analysis and complexity are different kinds of wrenches. The question is which one to use when, and how.

Complex Behavior or Complex System?
I’m not sure what the difference is between a “complex system” and “complex behavior”, but I am sure that unless I try to differentiate the two in my own mind, I’m going to get very confused. From what I have read in the evaluation literature, discussions tend to focus on “complex systems”, complete with topics such as parts, boundaries, part/whole relationships, and so on. My reading in the complexity literature, however, makes scarce use of these concepts. I find myself getting into trouble when talking about complexity with evaluators because their focus is on the “systems” stuff, and mine is on the “complexity” stuff. In these three blog posts I am going to concentrate on “complex behavior” as it appears in the research literature on complexity, not on the nature of “complex systems”. I don’t want to belabor this point because the boundaries are fuzzy, and there is overlap. But I will try to draw that distinction as clearly as I can.

What is the Contribution of Complexity to Evaluation?

In Part 2 I put considerable effort into explaining why programs tend to be based on simple behavior even though everyone knows that the problems those programs are trying to solve are embedded in complex dynamics. So, if we are evaluating programs on those terms, how can complexity be applied? The answer is that even if we are working within the “traditional” boundaries of program design, complex behavior is relevant. It may be hard to get people to design programs within a framework of complex systems, but it is eminently reasonable for evaluators to recognize that complex behavior may nevertheless be operating. Recognizing that relevance will allow us to produce much more powerful and relevant evaluation even when staying within those traditional boundaries of program design. In this section I hope to make this point with respect to three aspects of evaluation: 1) program theory, 2) methodology, and 3) measurement (in both quantitative and qualitative terms.)

Drawing from Research and Theory in Complexity Studies

I am about to pick and choose some ideas from complexity that I see as having particular relevance for evaluation. I make no claim to being comprehensive or systematic because it is hard to get a handle on what the field of “complexity” is. The difficulty is that ideas about “complexity” have been invented (discovered?) in many different fields, e.g. meteorology, biology, physics, mathematics, and human geography, to name but a few. Sometimes an idea pops up in one field and spreads to the others. Sometimes there is independent discovery. In either case, the people who do this work tend to define themselves in traditional disciplinary terms, as in: “I am a physicist who does research in complexity”, as opposed to: I am a “complexisist”. Maybe scientific work is moving in the direction of complexity as a recognized transdiscipline, but it’s not there yet, it may never get there, and I’m sure there are people who don’t think it should. As far as I can tell the best indicator is sociological. A concept is within the domain of “complexity” if people from different fields who claim to be studying complexity draw on that concept. Someday someone may come up with a GUT, but I’m not holding my breath.

Or, if you are not satisfied with the elaborate explanation in the previous paragraph, try this. I can only write about what I know, and what I know is limited.

Phase Shifts and Network Behavior

What happens to the contentedness of a network as pairs of nodes are randomly chosen and connected? This is a question that has been much studied in complexity research. The answer is that not very much happens until a critical value is reached, at which point there is a phase shift that rapidly connects almost all the nodes. To see a demo of this, download Net Logo and run the “giant component” model from the library. (It’s not as much fun because you can’t vary the parameters, but there is a nice You Tube demo as well.) See the picture for a screen shot.

What has this complexity behavior got to do with evaluation? I’ll illustrate with a hypothetical example I used in a workshop. The program was designed to promote healthy eating for adults in a small city. The intervention was at the level of civic organizations (churches, service clubs, etc.). There are two aspects to the program. First, the program provides a proven “best practice” curriculum for education and training about healthy eating, along with training on the content of the material and effective ways to deliver the classes. Second, the program provides technical assistance to help each service organization set up any program it wants to promote healthy eating in its community. There are no restrictions as to what the program can be as long as it is “on topic”, and can be produced and delivered with whatever resources (internal or externally supplied), the organization could muster.

How might all of these healthy eating programs affect the population? Here are two plausible ways to think of the program theory. Both are way oversimplified, I know. But stripped to their bare essentials, the difference between the two gets the message across.

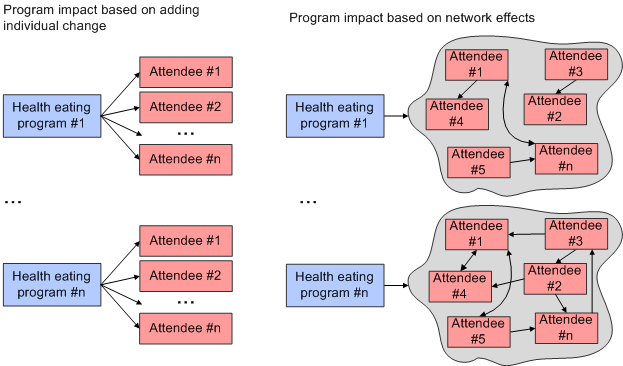
On the left, change takes place as individuals are influenced by the messages and the programs that emanate from the civic organizations. On the right, the mechanism of change is based on network effects. Here, individuals are directly influenced by what the civic organizations do, but they themselves in turn influence friends and family, who may then in turn influence their friends and family. One theory of change assumes that the dominant method of change is the sum total of influence of the program on individuals. I’ll call this the “program/individual” theory of change. The second theory of change assumes that if the programs are effective, it is because they support a network effect among individuals in the community. I’ll call this the “network” theory of change. (Let’s leave aside the question of which theory is correct, and the fact that in reality much more elaborate and mixed-mechanism changes are at play.) These two theories of change drive very different methodologies and a different sets of expectations about the pattern of change.

• The amount of change should vary reasonably evenly over time, thus if no change takes place soon after implementation, there is cause for concern.
• There is no need for data collection that will identify or map social influence network effects. Thus a very difficult, time consuming, and expensive data collection exercise is eliminated.

Network theory of change

• No change should be expected for quite some time, so no or minimal change as the program proceeds should not be too worrisome.
• Data collection methods are needed to map social influence dynamics. An elaborate, expensive, and time consuming evaluation exercise may be worthwhile.

Power and other Long Tail Distributions

Now let’s shift attention from the recipients of the health eating messages and turn to evaluation of the civic organizations themselves. One of the objectives of that program was to motivate civic organizations to deliver healthy eating programming. Therefore, it is reasonable to measure the civic organizations in terms of how many people they serve with their healthy eating programs.

At first blush one might think that the data would be normally (or at least symmetrically) distributed around a mean. Of course the distribution would be affected by the data on the left side of the mean being truncated by the zero point, but conceptually it would be “normal-like” in the sense of how organizations behaved in producing different numbers of healthy eating programs, and by extension, the number of participants in those programs. This is certainly a reasonable expectation based on a reasonable program theory. But consider another program theory based on some ideas that are prominent in studies of complexity.

Complexity researchers have come up with the notion of “preferential attachment” to explain network growth (and snowflake shape, and many other things.) Here is an idealized description of how it might be working with our civic organizations. Imagine that all the civic organizations in the community develop and advertise healthy eating programs. The public’s initial response is randomly distributed, with some programs drawing more people than others. So what do we have now? We have a second round of potential customers looking for healthy eating assistance. Where do they go? This time they look around and base their choice on what their friends and neighbors seem to prefer, i.e. the programs that are already most popular. And so it goes. Ultimately some programs will grow a lot, and some hardly at all. The result will be nothing like a normal distribution of people across civic organizations. (To see how this works with networks check out the demo, or just look at the picture.) Rather, the distribution will be power law. (In this case it really is a power law, but it’s entirely possible we will find program effects with long tail distributions that are not power laws. It’s actually not that easy to tell the difference. But that’s a complicated story that would take this discussion far-afield.

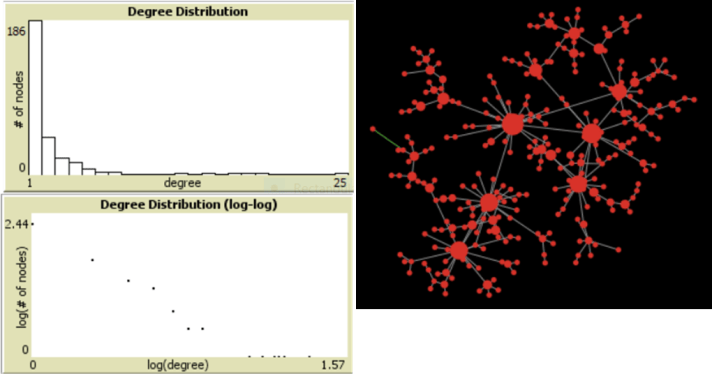
If the preferential attachment program theory is influencing outcomes, there are serious implications for evaluation. For instance:

• If we believed that only a very few organizations will be highly successful, it might be worth building in some in-depth study of what they did over time to assure that their popularity remained high.
• It might also be a good idea to watch for successful organizations that crashed and burned. What happened there?
• As for the funders, what view of “success” should they adopt? Perhaps they began with a vision of many program participants spread over many civic organizations. If so, maybe they should change that view. Maybe success should become doing something that can shift the inflection point on that top graph just a little bit to the right.
• From an analytical point of view, we would have to contend with the fact that power law distributions do not have well defined means, so different statistical methods would be needed to check for differences among groups.

Don’t misunderstand me. I’m not arguing that preferential attachment is a correct program theory for the scenario I described above. I’m only arguing that here is an idea in the “complexity domain” that is plausible enough to consider, and that if were to be considered, it would affect how the evaluation was done.

Attractors

Wikipedia  defines an “attractor” as follows:

“In dynamical systems, an attractor is a set of physical properties toward which a system tends to evolve, regardless of the starting conditions of the system. Property values that get close enough to the attractor values remain close even if slightly disturbed.”

Wikipedia then goes on to explain a whole variety of attractor types that you can read about if you are interested. For me though, thinking as an evaluator, the important point is that an attractor can be thought of as the “space” within which entities are found. After a while, any entity that was pushed outside that space will end up back in it. Obvious physical examples would be the arc of a swinging pendulum, or the orbit of a planet.

But the notion of an attractor can also apply to the world that we evaluators live in. What does it mean to say that “Power tends to corrupt, and absolute power corrupts absolutely.”? What are we to make of the common evaluation finding that sustainability is difficult, i.e. that once special funding and attention go away, things go back to the way they were? How can we explain historical policy changes in regulatory agencies that seem to oscillate between rule enforcement and a cooperative, collaborative approach to the industries they are responsible for? One could think of these cases in terms of types of attractors. In the “power” example there is inevitable and continual travel from any point on a line to other points to the right of the starting point. The “sustainability” example looks like the bottom of a basin of attraction. Remove the energy, and an entity will gravitate to the bottom. The “regulatory” example seems like a pendulum.

The reason I like the notion of an “attractor” is that it provides a framework for thinking about system change in a way that indicates (I hesitate to say “predicts”) likely change for whole classes of systems. For instance, many programs (with different missions and organizational/political contexts) might be seen as living at the bottom of a basin of attraction. Many agencies with some regulatory function might be understood as living on that pendulum. So as an evaluator, I reap two benefit. First, I have some idea of what might be an “unexpected” event in the life of the program I am evaluating. Second, I know where to look for other similar programs.

Of course there are other ways to think about any of the examples I just discussed. Here are a few. “Power” can be analyzed in terms of psychology. “Stability” in terms of “institutional inertia”, or “resistance to change”. “Regulatory” in terms of the limits of either tactic combined with the likelihood of high profile failures. There is nothing wrong with looking at change in these ways. I do it all the time myself. My only point is that thinking in terms of attractors can be a useful aspect of program theory. It is a powerful notion from the study of complexity that can be used in evaluation.

Strange Attractors

There are many explanations of strange attractors to be found. The one that is most useful for me is:

“When a bounded chaotic system does have some kind of long term pattern, but which is not a simple periodic oscillation or orbit we say that it has a Strange Attractor. If we plot the system’s behaviour in a graph over an extended period we may discover patterns that are not obvious in the short term. In addition, even if we start with different initial conditions for the system, we will usually find the same pattern emerging. The area for which this holds true is called the basin of attraction for the attractor.

This is a fancy way of saying that there is chaotic behavior within some bounded space . That means you can’t ever say where the position of a point will be based on knowledge of its immediate prior position, but you can know for certain the shape of the space in which the point will exist. (Strange attractors are also fractal in the sense that the same pattern of bounded chaos shows up as one zooms in and out of the measurement scale. That is truly interesting, but I can’t see any relevance for the work I do.)

Wikipedia has some nice graphics and demos to illustrate chaotic behavior in a bounded space. One good one is the Lorenz attractor, see the butterfly. Another nice example is the movement of the double compound pendulum. Ignore the depiction of chaos in Greek mythology. That’s another kind of strange attractor.

 

For me the idea of a strange attractor is a useful metaphor for many evaluation situations. We don’t seem to be able to specify exactly what path a program will take or exactly what it will accomplish, but we do know that it’s not random in the sense that we can say nothing about it, or that the best we can do is to express its behavior strictly is statistical terms. In one sense the program and its outcomes are highly predictable despite very sharp limits on what we can know about it. That seems very strange attractor-like to me.

In reality a great many evaluations recognize this principle. Think of the frequently used Kellogg logic model, with its lists of inputs, activities, outputs, outcomes, and impacts. That model never specifies what the relationships need to be within any given category in order to have some effect on the succeeding category. Nor does it specify exactly which changes will take place. It only specifies a set of possibilities. The message is: If a lot of stuff will happen here, a lot of stuff will happen there”. Take the “outcomes” category for example. What the model specifies is a set of possible outcomes, or in complexity terms it specifies the “state space” in which an outcome will be found. But exactly where? Who knows, because the answer is sensitively dependent on what happened in the preceding part of the model.

As another example, I’ll steal from one of my previous blog posts. I cooked up a hypothetical example that a friend in the field of educational evaluation assures me is not too far off the wall. Imagine an innovative program to help teachers do better classroom management. Let’s assume the program works, i.e. teachers do in fact get better at managing their classrooms. Let’s also assume the effect is fairly robust, i.e. it helps most teachers, in a wide variety of teaching environments, to do better classroom management. What outcomes might ensue? 1) More teacher job satisfaction. 2) Greater student satisfaction with being in class. 3) Higher scores on various tests. 4) More homework completion. 5) Fewer absences. 6) Less tension between teachers and principals. 7) Better interaction between teachers and parents. 8) More on-task behavior by students during class. 9) Fewer disruptive students. This is not a complete set, and some are more likely than others. But with enough empirical research across classroom settings, a pretty complete list could be developed.

What cannot be developed, though, is knowledge of which effects will show up where, or which particular effects interact with others to bring still others about. For instance, in one case student satisfaction and more homework completion may combine to improve test scores. In another, parent involvement and on-task behavior may have been the reasons for higher test scores. In another case student satisfaction and less classroom disruption might combine to improve teacher satisfaction, which would then lead to higher test scores. And so on and so forth. In any given classroom there will be a Gordian know of relationships among outcomes that can never be untangled. (See the pictures for an illustration of what the logic model might look like.) What we do know however, is the set of outcomes that can be expected. That’s bounded chaos-like. That’s a strange attractor-like. That’s a pretty decent level of predictability with all manner of implications for methodology, policy making, and estimating educational impact.

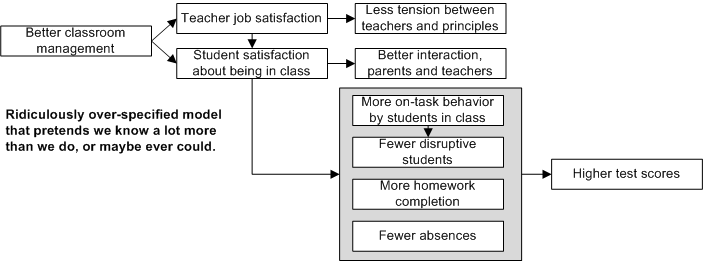
If the metaphor of a “strange attractor” for evaluation outcomes makes sense, it has big implications for program theory and for stakeholder expectations because it means that it is possible to specify a set of likely outcomes for program, but that it is possible to assert that if the program works, a particular group of outcomes will occur. Stakeholders will have to be satisfied with a pretty high level of predictive power, but a type of prediction that is highly constrained. Precisely which outcomes may show up? What pattern of program activity will lead to those outcomes? These are not difficult questions to answer. They are impossible question to answer.

Obviously there are also implications for methodology and for drawing inference from data. Here are a few that spring to mind. The program theory provides no guidance as to when particular measurements should be taken, rather, all the possible outcomes need to be assessed from the beginning. It is possible to determine the causal sequence in any particular implementation of the program. That knowledge can provide insight about what may happen the next time, but no prescriptive guidance. Quite a lot of close observation and interviewing will be needed if stakeholders do care about the causal relationships among outcomes.

Emergence and Agents

All the other sections in this blog post discuss practices that any traditionally trained evaluator can apply using the knowledge and expertise that he or she already has. This section is different because it gets into topics that are alien both to the training we received in graduate school, and to the everyday work that we do. I don’t know too many people who are working in this area. If you are one, get in touch with me. I’d love to talk.

Wikipedia defines Emergence as follows:

In philosophy, systems theory, science, and art, emergence is the way complex systems and patterns arise out of a multiplicity of relatively simple interactions.

What this means is that emergence is a phenomenon in which the behavior of the system as a whole is not explicit in the behavior of its components. This statement has to be understood in a different way than our common sense understanding of parts and wholes. An example is the common sense understanding of a “school”. A school cannot be understood by looking only at students, teachers, principals, curricula, testing, parents associations, sports teams, and all the other inter-related parts and processes that make up the school as a system. Each of those parts is different from each of the others. “Students”, “classes” and “testing procedures” are not interchangeable components. The whole is different than its individual parts because the idea of a “sum of parts” makes no sense. Why does it make no sense? Because of the numerous continually fluctuating relationships among those parts, a “school” is what we would colloquially call a “complex system”. In common parlance we may say that the school is an example of emergent behavior. The essence of the “school” emerges from the relationships among its components. This is a reasonable understanding of the notion of “emergence”. It is not, however, “emergence” in complexity terms. There, it means something entirely different.

To illustrate what “emergence” means in complexity terms, consider the beehive. Beehives perform sophisticated functions – physical construction of an elaborate nest, task allocation across workers, temperature regulation – that are not explicit in the behavior of any single bee. Rather, something happens when the “agents” (in this case bees) interact to result in, to make “emerge,” an elaborate structure. The simple bees interact based on well-defined rules, and out of the interaction comes the elaborate beehive. (Lest you think that all this stuff isy only relevant to bees, go to the social science section of the Net Logo models library.) In complex systems, agents can take any form that can act “as if” they can sense their environment and apply behavioral rules based on those perceptions. An agent can be anything – bees, classrooms, teachers, school districts, county governments, and much else besides.

“Emergence” can lead to extremely predictable explanations of how social phenomena take place. Those explanations, however, are fundamentally different from how people in our business think of program theory. To see a nice demo of this, play the segregation game. There you will see integrated neighborhoods segregate when each agent (aka family) in the neighborhood follows a few simple rules: 1- Decide how many of your neighbors should be like you. 2- Look around. 3- If not enough of your neighbors are like you, move. 4- Repeat steps 1 – 3 until the number of your neighbors meets your comfort level. If agents are randomly dropped into the neighborhood and follow these rules, the neighborhood segregates.

What are we to make of this simulation? I don’t know if that is how the real world works. I do know that if I were to try to explain neighborhood segregation, I would think of a lot of reasons other than those few simple rules, e.g. housing values, schools, lending practices, history of racial tensions among various groups, crime rates, gentrification, and so on. But would it be a good idea to base my evaluation on a program theory that ignored emergence based on agent behavior as a possible explanation? As a minimum, wouldn’t it be a good idea to think about partitioning all those factors into ones that might be drivers of “decide how many of your neighbors should be like you”? I’m not advocating searching for agent-based emergence in every nook and cranny of our program theories. I only want to make the point that “emergence” is one of the many ideas in the field of complexity that are worth considering when we do evaluation.

Agent Based Simulation

The discussion above leads me to advocate for the methodology of agent-based simulation. I am not advocating that a lot of evaluators go out and learn how to do this. I would no sooner make such an argument as I would propose that all of start to use analytical hierarchy process, big data analytics, Bayesian statistics, or any of the other multitudinous methods that might be useful for us, but which we seldom use. What I am going to do is advocate for the presence of the method within the field of evaluation.

I think the quiver of evaluation tools needs to include agent based simulation. The reason for my opinion is that “emergence” is a truly important idea in program theory, and there is no way to study emergence without agent based simulation. To illustrate, go back and look at the segregation game. There is some useful insight in seeing how those simple rules can move families about. More insight can be gained by playing with the rules. For instance, what would happen if on a random basis, some families decided to stay put no matter what the color of their immediate neighbors? What if we established a “gentrification” parameter that affected the environment in which the families lived? I have no idea what the answers to these questions would be, but I do know that I’d get a lot of good ideas about evaluating neighborhood development programs if I did know the answers.

Another reason for considering agent based simulation is because it can be used to good advantage in concert with the traditional logic models and program theories that we employ all the time. (A case can be made for using system dynamic models for this purpose as well, and endless interesting conversation can be had about the pros and cons of each approach. But the discussion would take this blog post way too far-afield, so I will say no more about it now.)

To see an example of how these methods can be combined, see Agent Simulation. It’s a You Tube video that shows what my colleague Van Parunak and I have been working on. What you will see is that by doing the simulation, it is possible to question assumptions and develop evaluation approaches in ways that would not happen using our traditional methods alone. Thanks to the Faster Forward Fund we have brought two new people into the fold (Kirk Knestis and Melanie Hwalek), and are extending this work with some new data sources. Stay tuned for some more You Tube presentations.